Recurrent Neural Networks
Here we implement a simple recurrent neural network (Elman network [Elm]) with theano.
Characteristica of recurrent neural networks:
- high-dimensional hidden state (distributed representation)
- non-linear dynamics
- RNN with standard linear connections are computationally as powerful as any turing machine [SiSo91]
Forward Pass
- Sequence of input vectors: $\vec{x}_1, \dots , \vec{x}_T$
- Hidden vectors: $\vec{h}_1, \dots , \vec{h}_T$
- Output Vectors: $\vec{o}_1, \dots , \vec{o}_T$
The parameter of the recurrent neural network:
- Input-hidden connection matrix: $W_{ih}$
- Biases of the hidden neurons: $\vec{b}_h$
- Hidden-hidden connection matrix: $W_{hh}$
- Biases of the output neurons: $\vec{b}_o$
- Hidden-output connection matrix: $W_{ho}$
The state of the hidden neurons at a time step $t$ is computed by: $$ \vec{h}_t = act_h (\vec{x}_{t} W_{ih} + \vec{h}_{t-1} W_{hh} + \vec{b}_h) $$
The state of the outputs is given by: $$ \vec{o}_t = act_o (\vec{h}_t W_{ho} + \vec{b}_o) $$
Remark: In the formulars above the vectors are row vectors. There is a little difference to the usual formulations where the vectors are column vectors. The reason is that in nearly all theano code examples a matrix-vector product is written as T.dot(input, self.W). Note that the following relation holds:
$$ (\vec x W_{xy})^T = W_{xy}^T \vec{x}^T = W_{yx} \vec{x}^T = W_{yz} \vec{z} $$ $\vec z$ is a column vector and $\vec x$ the corresponding row vector ($\vec z^T = \vec x$ ).
Enrolling in time
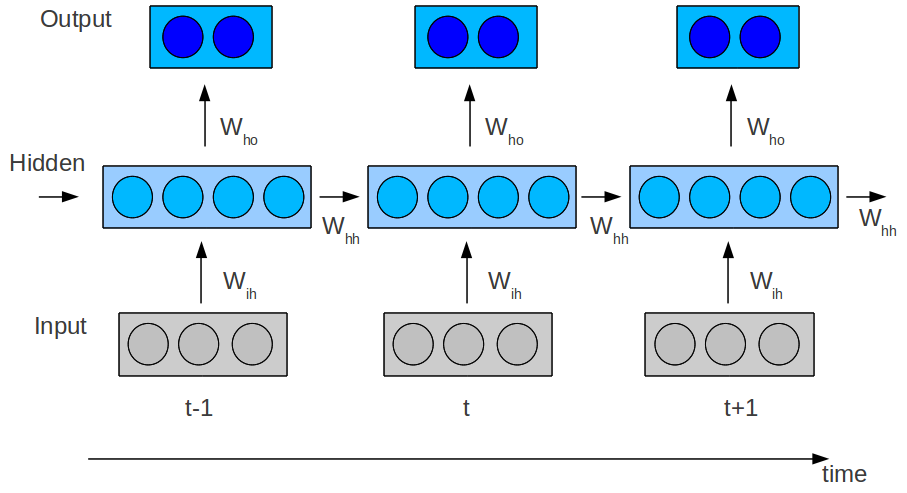
The hidden state at $t=0$ can also be learned and can be considered as a parameter of the rnn.
Backward Pass
Enrolling the recurrent neural network in time allows to apply gradient descent learning similar to feed forward neural networks.
Here we construct an expression graph with theano which takes care of computing the gradient and updating the weights.
Implementation with Theano
import numpy as np
import theano
import theano.tensor as T
dtype=theano.config.floatX
We use the reber grammar data (see reber grammar), so the dimension of the layers are:
import reberGrammar
n_in = 7
n_hid = 10
n_out = 7
To keep things simple we have just one example $\vec v$ for each time stept $t$. So all inputs can be written as a Matrix:
#first dimension is time
v = T.matrix(dtype=dtype)
Because the vanishing and exploding gradient depends on the largest singular value (see [Pas13]), we
initialize the weights fixing the largest singular value (for the tanh) to 1 [similar in groundhog]:
def rescale_weights(values, factor=1.):
factor = np.cast[dtype](factor)
_,svs,_ = np.linalg.svd(values)
#svs[0] is the largest singular value
values = values / svs[0]
return values
def sample_weights(sizeX, sizeY):
values = np.ndarray([sizeX, sizeY], dtype=dtype)
for dx in xrange(sizeX):
vals = np.random.uniform(low=-1., high=1., size=(sizeY,))
#vals_norm = np.sqrt((vals**2).sum())
#vals = vals / vals_norm
values[dx,:] = vals
_,svs,_ = np.linalg.svd(values)
#svs[0] is the largest singular value
values = values / svs[0]
return values
Parameter
The parameters of the RNN are defined as theano shared variables:
# parameters of the rnn as shared variables
def get_parameter(n_in, n_out, n_hid):
b_h = theano.shared(np.zeros(n_hid, dtype=dtype))
h0 = theano.shared(np.zeros(n_hid, dtype=dtype))
W_ih = theano.shared(sample_weights(n_in, n_hid))
W_hh = theano.shared(sample_weights(n_hid, n_hid))
W_ho = theano.shared(sample_weights(n_hid, n_out))
b_o = theano.shared(np.zeros(n_out, dtype=dtype))
return W_ih, W_hh, b_h, W_ho, b_o, h0
W_ih, W_hh, b_h, W_ho, b_o, h0 = get_parameter(n_in, n_out, n_hid)
params = [W_ih, W_hh, b_h, W_ho, b_o, h0]
Basis of the implementation with theano is the scan operator.
Scan takes a function which is computed at each iteration step.
# we could use the fact that maximaly two outputs are on,
# but for simplicity we assume independent outputs:
def logistic_function(x):
return 1./(1 + T.exp(-x))
# sequences: x_t
# prior results: h_tm1
# non-sequences: W_ih, W_hh, W_ho, b_h
def one_step(x_t, h_tm1, W_ih, W_hh, b_h, W_ho, b_o):
h_t = T.tanh(theano.dot(x_t, W_ih) + theano.dot(h_tm1, W_hh) + b_h)
y_t = theano.dot(h_t, W_ho) + b_o
y_t = logistic_function(y_t)
return [h_t, y_t]
Scan iterates through the sequences and compute a function at each iteration step. The four parameters (that we use) for scan are:
fn: The function which is computed at each time stepsequences: The sequence input to the functionfnoutputs_info: Initialization of the iteration. We provide onlyh0. Must corresponds to the return type offn, so we provide alsoNone.non_sequences: Variables that are used as additional input at each timestep.
Note that the parameter of the function fn (here one_step) are: sequences, prior results and non-sequences in exact this order.
# hidden and outputs of the entire sequence
[h_vals, o_vals], _ = theano.scan(fn=one_step,
sequences = dict(input=v, taps=[0]),
outputs_info = [h0, None], # corresponds to return type of fn
non_sequences = [W_ih, W_hh, b_h, W_ho, b_o] )
The target values are also given as matrix:
# target values
target = T.matrix(dtype=dtype)
We learn the net with stochastic gradient decent with the learning rate as hyperparameter of the training procedure. Theano takes care of backpropagation through time.
# learning rate
lr = np.cast[dtype](0.2)
learning_rate = theano.shared(lr)
We do classification therefore the cost function is the mean of the cross entropy losses (for the independent-outputs simplification) for all time steps .
cost = -T.mean(target * T.log(o_vals) + (1.- target) * T.log(1. - o_vals))
def get_train_functions(cost, v, target):
gparams = []
for param in params:
gparam = T.grad(cost, param)
gparams.append(gparam)
updates=[]
for param, gparam in zip(params, gparams):
updates.append((param, param - gparam * learning_rate))
learn_rnn_fn = theano.function(inputs = [v, target],
outputs = cost,
updates = updates)
return learn_rnn_fn
learn_rnn_fn = get_train_functions(cost, v, target)
Let's generate some training data. Here we use the reberGrammar (you must copy the code in a file reberGrammar.py for the import!):
import reberGrammar
train_data = reberGrammar.get_n_examples(1000)
def train_rnn(train_data, nb_epochs=50):
train_errors = np.ndarray(nb_epochs)
for x in range(nb_epochs):
error = 0.
for j in range(len(train_data)):
index = np.random.randint(0, len(train_data))
i, o = train_data[index]
train_cost = learn_rnn_fn(i, o)
error += train_cost
train_errors[x] = error
return train_errors
nb_epochs=10
train_errors = train_rnn(train_data, nb_epochs)
%matplotlib inline
import matplotlib.pyplot as plt
def plot_learning_curve(train_errors):
plt.plot(np.arange(nb_epochs), train_errors, 'b-')
plt.xlabel('epochs')
plt.ylabel('error')
plot_learning_curve(train_errors)
Predictions
For the predictions we need to compile a new function.
predictions = theano.function(inputs = [v], outputs = o_vals)
inp, outp = reberGrammar.get_one_example(10)
pre = predictions(inp)
for p, o in zip(pre, outp):
print p # prediction
print o # target
print
Sampling
In many cases it's interesting to generate sequences from recurrent neural networks. Let's sample from the trained rnn to produce reber grammar strings.
from theano.tensor.shared_randomstreams import RandomStreams
srng = RandomStreams(seed=234)
def get_sample(probs):
return srng.multinomial(n=1, pvals=probs)
# sequences:
# prior results: h_tm1, y_tm1
# non-sequences: W_ih, W_hh, W_ho, b_h
def sampling_step(h_tm1, y_tm1, W_ih, W_hh, b_h, W_ho, b_o):
h_t = T.tanh(theano.dot(y_tm1, W_ih) + theano.dot(h_tm1, W_hh) + b_h)
y_t = theano.dot(h_t, W_ho) + b_o
y_t = logistic_function(y_t)
# normalize probabilities to all outputs
y_t = y_t / T.sum(y_t)
y_t = get_sample(y_t)
y_t = T.cast(y_t, dtype)
return [h_t, y_t], theano.scan_module.until(y_t[6]>.99)
# always start with B-Symbol
#y0 = T.constant(np.array([1,0,0,0,0,0,0], dtype=dtype))
y0 = theano.shared(np.array([1.,0.,0.,0.,0.,0.,0.], dtype=dtype))
# hidden and outputs of the entire sequence
[h_vals, y_vals], updates = theano.scan(fn=sampling_step,
sequences = [],
n_steps = 10000,
outputs_info = [h0, y0], # corresponds to return type of fn
non_sequences = [W_ih, W_hh, b_h, W_ho, b_o] )
samples = theano.function(inputs = [], outputs = y_vals, updates=updates)
# TODO get rid of this warning message!?
for i in range(20):
sample_sequence = np.concatenate((np.array([[1.,0.,0.,0.,0.,0.,0.]], dtype='float32'), samples()), axis=0)
word = reberGrammar.sequenceToWord(sample_sequence)
print "inGrammar(",word,") = ", reberGrammar.in_grammar(word)
As you can see most of the generated strings are in the grammar. With a little bit of tuning it should be possible to produce mainly correct reber strings.
Long-range dependencies
Contrary to the reber grammar the embedded reber grammar data set has a long range dependency: The second symbol is the same as the second to last symbol.
i, o = reberGrammar.get_one_embedded_example()
print i[1]
print o[-2]
This long range dependency can not be trained effectively with an elman net by backpropagation-through-time, because of the vanishing gradient problem [H91]:
W_ih, W_hh, b_h, W_ho, b_o, h0 = get_parameter(n_in, n_out, n_hid)
params = [W_ih, W_hh, b_h, W_ho, b_o, h0]
# hidden and outputs of the entire sequence
[h_vals, o_vals], _ = theano.scan(fn=one_step,
sequences = dict(input=v, taps=[0]),
outputs_info = [h0, None], # corresponds to return type of fn
non_sequences = [W_ih, W_hh, b_h, W_ho, b_o] )
cost = -T.mean(target * T.log(o_vals)+ (1.- target) * T.log(1. - o_vals))
learn_rnn_fn = get_train_functions(cost, v, target)
train_data = reberGrammar.get_n_embedded_examples(1000)
train_errors = train_rnn(train_data)
predictions = theano.function(inputs = [v], outputs = o_vals)
i, o = reberGrammar.get_one_embedded_example()
print i[1]
print o[-2]
print predictions(i)[-2]
Note that the second and fifth input/output neuron code for the two embedding symbols have high probability (about 50%) nearly independent of the correct output.
A solution for this problem is the LSTM recurrent neural network.
Exercise: Scan Operator
The data (inputs and targets) are now 3d tensors with the sequence index as first dimension:
x = np.array(np.arange(0., 2 * np.pi, 0.2), dtype=dtype)
x = x.reshape(len(x), 1)
s_ = np.concatenate([np.sin(x), np.cos(x)], axis=1)
sh_ = np.roll(s_, 1, axis = 0)
S_ = np.array([s_,sh_])
T_ = np.roll(S_, 1 , axis=1)
The input is S_ and the output T_:
V = T.tensor3(dtype=dtype)
Ta = T.tensor3(dtype=dtype)
For educational purposes you should nest scan in the exercise to get more familiar the theano scan.
Solution
n_in = 2
n_hid = 4
n_out = 2
W_ih, W_hh, b_h, W_ho, b_o, h0 = get_parameter(n_in, n_out, n_hid)
params = [W_ih, W_hh, b_h, W_ho, b_o, h0]
# learning rate
lr = np.cast[dtype](.1)
learning_rate = theano.shared(lr)
# sequences: x_t
# prior results: h_tm1
# non-sequences: W_ih, W_hh, W_ho, b_h
def one_step(x_t, h_tm1, W_ih, W_hh, b_h, W_ho, b_o):
h_t = T.tanh(theano.dot(x_t, W_ih) + theano.dot(h_tm1, W_hh) + b_h)
y_t = theano.dot(h_t, W_ho) + b_o
# no squashing for the output - it's a regression task
return [h_t, y_t]
Scan iterates over the leading dimension of the sequences.
def loop_over_examples(x):
# hidden and outputs of the entire sequence
[h_vals, o_vals], _ = theano.scan(fn=one_step,
sequences = dict(input = x, taps=[0]),
outputs_info = [h0, None], # corresponds to return type of one_step
non_sequences = [W_ih, W_hh, b_h, W_ho, b_o]
)
return o_vals
# return y_vals
O_vals, _ = theano.scan(fn = loop_over_examples,
sequences = dict(input = V, taps=[0]),
outputs_info = None
)
f = theano.function(inputs=[V], outputs=O_vals)
# It's a regression task, so the cost is the mean of the squared error losses:
cost = ((O_vals - Ta)**2).mean()
gparams = []
for param in params:
gparam = T.grad(cost, param)
gparams.append(gparam)
updates=[]
for param, gparam in zip(params, gparams):
updates.append((param, param - gparam * learning_rate))
learn_rnn_fn = theano.function(inputs = [V, Ta],
outputs = cost,
updates = updates)
for i in xrange(10000):
train_cost = learn_rnn_fn(S_,T_)
train_cost
predictions = theano.function(inputs = [V], outputs = O_vals)
P = predictions(S_)
P - T_
Literatur
- [Pas13] Razvan Pascanu, Tomas Mikolov, Yoshua Bengio: On the difficulty of training Recurrent Neural Networks, ICML 3, volume 28 of JMLR Proceedings, page 1310-1318. JMLR.org, (2013)
- [SiSo91] Hava T. Siegelmann , Eduardo D. Sontag: Turing Computability With Neural Nets, Applied Mathematics Letters 1991
- [Elm90] Jeffrey L. Elman: Finding Structure in Time. Cognitive Science, 14, 1990
- [H91] S. Hochreiter. Untersuchungen zu dynamischen neuronalen Netzen. Diploma thesis, Institut f. Informatik, Technische Univ. Munich, 1991. Advisor: J. Schmidhuber