Programming Models for Deep Learning and Deep Learning Frameworks¶
incl. explaination of Backpropagation and Autodiff
with examples in Theano and TensorFlow
Model specification¶
(from mxnet documentation)
- per configuration
- inflexible, just reuse of common building blocks
- examples: Caffe, CNTK
- programmatic
- flexible, programming of building blocks possible
- examples: Torch, Theano, Tensorflow, MXnet
Imperative¶
Imperative style programs conduct the computation as we run them.
import numpy as np
a = np.ones(10)
b = np.ones(10) * 2
c = b * a # when the programs execute to c = b * a,
#it runs the actual computation.
d = c + 1
Symbolic¶
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
# compiles the function
f = compile(D)
d = f(A=np.ones(10), B=np.ones(10)*2)Computational Graph¶
The difference in symbolic programs is when C = B * A is executed, there is no actual computation happening. Instead, these operations generate a computation graph (symbolic graph) that represents the computation it described.
AandBare symbolic variables or symbols
from IPython.display import Image
Image(filename='./pics/comp_graph.png', height=400)
# image from the mxnet documentation
Most symbolic style programs contain, either explicitly or implicitly, a compile step.
Theano¶
import theano.tensor as T
from theano import function
# in theano each symbolic variable must be assigned a tensor (shape) type and data type
A = T.dscalar('A') # default of dtype is floatX
print ("A.dtype:", A.dtype)
B = T.dscalar('B')
C = T.mul(B, A)
D = C + 1
f = function(inputs=[A, B], outputs=D) # compile a function
f(1,2)
# implicit compilation with theano
Z = T.add(A+B) * 3.
Z.eval({A:2., B:5.})
Tensorflow¶
import tensorflow as tf
# if no graph is specified the default graph is used
# tf.placeholder for defining symbolic variables
A = tf.placeholder(name="A", dtype=tf.float32)
B = tf.placeholder(name="B", dtype=tf.float32)
C = tf.multiply(B, A, name="multiplication")
D = C + 1
with tf.Session() as sess:
result = sess.run([D], feed_dict={A:1., B:[2.]})
print(result)
tf.get_variable?
Graph in Tensorflow¶
g = tf.get_default_graph()
[op.name for op in g.get_operations()]
# write the definition of the graph to the log file
writer = tf.summary.FileWriter("./tmp/graph_logs",
tf.get_default_graph())
writer.flush()
Lanch tensorboard on the commandline:
>tensorboard --logdir=tmp/graph_logs/
Starting TensorBoard 23 on port 6006
(You can navigate to http://0.0.0.0:6006)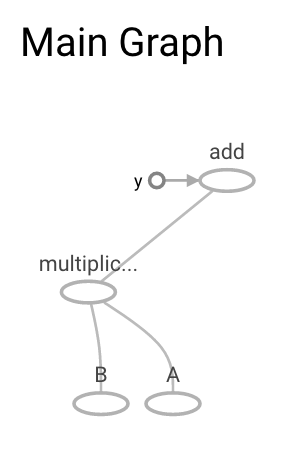
Shared Variables¶
In Neural Networks learning is (mostly) optimization of parameters.
Values of variables are hold during execution of the computational graphs.
e.g. with a numpy array W_value.
Theano: Shared Variables
weights = theano.shared(value=W_values, name='weights')Tensorflow: Variables
weights = tf.Variable(initial_value=W_values, name='weights')create a new variable every time it is called
or
weights = tf.get_variable(name='weights', initializer= )also be used for weight sharing
Name and Variable Scope¶
Note: In tensorflow the names of variables and operators can be automatically prefixed (hierarchically) by
with tf.name_scope("first_layer") as scope:
...
The names of the variables (tf.get_variable(..)!) (and operators) can be automatically prefixed (hierarchically) by
with tf.variable_scope("first_layer") as scope:
...
reuse=False: gives an exception if a variable name is used again.reuse=True: for sharing weights.
for the difference between tf.name_scope and tf.variable_scope see e.g. stackoverflow
with tf.variable_scope("foo"):
with tf.variable_scope("bar", reuse=None):
q = tf.get_variable(name="q", shape=[1])
assert q.name == "foo/bar/q:0"
with tf.name_scope("foo"):
with tf.variable_scope("bar", reuse=None):
p = tf.Variable(name='p', initial_value=[1])
u = tf.get_variable(name='u', shape=[1]) # the foo scope is ignored
print (p.name)
print (u.name)
Constant¶
Python and numpy numbers are wrapped automatically in the constant type. Here explicit with a name for the constants:
Theano
T.constant(np.ones([2,3]), name="a_constant")
Tensorflow
tf.constant(np.ones([2,3]), name="a_constant")
Loops¶
Imperative Programs¶
- (mostly) more flexible
x = 2
k = 10
result = 1
# compute x**k by a python loop
for i in range(k):
result = result * x
print (result)
Python for-loop can not be used directly in the symbolic API.
(Loops may not readily supported by some symbolic API).
Loops in Theano¶
In Theano and TensorFlow the scan-Operator is used for loops.
Theano example from http://deeplearning.net/software/theano/library/scan.html
import theano
import theano.tensor as T
k = T.iscalar("k")
A = T.iscalar("A")
There are three things here that we need to handle:
- the initial value assigned to result
- the accumulation of results in result, and
- the unchanging variable A. Unchanging variables are passed to
scanasnon_sequences. Initialization occurs inoutputs_info, and the accumulation happens automatically.
# Symbolic description of the result
result, updates = theano.scan(fn=lambda prior_result, A: prior_result
* A,
outputs_info=T.ones_like(A),
non_sequences=A,
n_steps=k)
# Note that the result is not a matrix, but a 3D tensor containing the value of A**k for each step.
# We want the last value (after k steps) so we compile a function to return just that.
# We only care about A**k, but scan has provided us with A**1 through A**k.
# Discard the values that we don't care about. Scan is smart enough to
# notice this and not waste memory saving them.
final_result = result[-1]
# compiled function that returns A**k
power = theano.function(inputs=[A, k],
outputs=final_result, updates=updates)
# note A is a T.vector, as input a np-vector or a python list is OK:
print (power(2, 10))
Function that is given to scan:
fn=lambda prior_result, A: prior_result * A
The order of parameters is fixed by scan: the output of the prior call to fn
(or the initial value, initially) is the first parameter, followed by all non-sequences.
# Example compute x**k by a python loop
k = 10
x = 2
out = tf.scan(lambda previous_output, current_input:
previous_output * current_input,
tf.fill([k], x), initializer=tf.constant(1))
with tf.Session() as sess:
sess.run(tf.initialize_all_variables())
print(sess.run(out[-1]))
# example cummulative sum
elems = tf.Variable([1.0, 2.0, 2.0, 2.0])
elems = tf.identity(elems)
initializer = tf.constant(0.0)
out = tf.scan(lambda previous_output, current_input: previous_output + current_input,
elems, initializer=initializer)
with tf.Session() as sess:
sess.run(tf.initialize_all_variables())
print(sess.run(out))
#tf.scan?
Symbolic programs vs. imperative programs (as native python)¶
from the nxnet documentation
If you are writing a symbolic programs in python, you are NOT writing in python. Instead, you actually write a domain specific language defined by the symbolic API. The symbolic APIs are more powerful version of DSL that generates the computation graphs or configuration of neural nets. In that sense, the config-file input libraries are all symbolic.
Because imperative programs are actually more native than the symbolic ones, it is easier to use native language features and inject them into computation flow. Such as printing out the values in the middle of computation, and use conditioning and loop in host language.
Symbolic programs are more efficient in memory and runtime.
- intermediate values of computation are invisible to the user
- re-use memory by in-place computation.
Optimization that symbolic programs can do is operation folding.
The way optimizations work in Theano is by identifying and replacing certain patterns in the graph with other specialized patterns that produce the same results but are either faster or more stable.
In the above programs, the multiplication and addition can be folded into one operation. Which is represented in the following graph. This means one GPU kernel (e.g. cuda kernel) will be executed(instead of two) if the computation runs on GPU. Doing so will improve the computation efficiency.
from IPython.display import Image
Image(filename='./pics/comp_graph_fold.png', height=400)
# from the mx net documentation
Gradient Calculation by Backpropagation¶
- for efficient calculation of the gradient
If for each operator the (partial) derivative is defined, gradients of the computation graph can be computated automatically by backpropagation (application of the chain rule).
(Recursive application) of the chain rule¶
Chain rule for a function $c(b(w))$ ($c$ is a function of $b$ and $b$ is a function of $w$):
$$ \frac{\partial c(b(w))}{\partial w} = \frac{\partial c(b(w))}{\partial b} \frac{\partial b(w)}{\partial w} $$Sum rule and product rule¶
if $b$ is not a function of $u$:
$$ \frac{ \partial (a b)}{\partial u} = \frac{\partial a}{\partial u} b + a \frac{\partial b}{\partial u} = \frac{\partial a}{\partial u} b $$$$ \frac{ \partial (a(u) + b)}{\partial u} = \frac{\partial a}{\partial u} $$Backpropagation¶
If we have a computational graph to compute $c$ and two parameters in the graph $v$ and $w$, e.g. the following computational graph:
o1 (name='c')
/ \
/ \
/ z
/
o2 (name='b')
/ \
/ \
/ y
/
o3 (name='a')
/ \
/ \
w vo1,o2 and o3 are arbitrary operators, $y$ and $z$ and branches of the tree.
And we want to compute the two partial derivatives $\frac{\partial c(b(a(w, v)))}{\partial w}$ and $\frac{\partial c(b(a(w, v)))}{\partial v}$.
Note that the application of the chain rule results in:
$$ \frac{\partial c(b(a(w, v)))}{\partial w} = \frac{\partial c(b)}{\partial b}\frac{\partial b(a)}{\partial a} \frac{\partial a(w,v)}{\partial w} $$$$ \frac{\partial c(b(a(w, v)))}{\partial v} = \frac{\partial c(b)}{\partial b}\frac{\partial b(a)}{\partial a} \frac{\partial a(w,v)}{\partial v} $$The first two factors of both expressions are the same. So we need to compute them only once. That's the key idea of back propagation. We need to compute such factors only once and can backpropagate them through the graph.
Example for the given operator graph:
Assume e.g. o1 and o3 is a multiplication ($*$) and o2 is an add-Operator ($+$).
Application of the chain rule ($z$ is not a function of $w$):
so we have:
$$ \frac{\partial c}{\partial w} = z * 1 * v = z * v $$For $\frac{\partial c}{\partial v}$ the first to factors of the chain rule ('$z$' and '1') are the same and we can reuse it.
$$ \frac{\partial c}{\partial v} = z * 1 * \frac{\partial a(v)}{\partial w} = z * 1 * w = z * w $$Example implementation of autodiff (imperative)¶
Reverse mode differentiation.
Multivariable Chain Rule¶
$$ \frac{\partial}{\partial t} f(x(t), y(t)) = \frac{\partial f}{\partial x} \frac{\partial x}{\partial t}+ \frac{\partial f}{\partial y}\frac{\partial y}{\partial t} $$If there are multiple paths to a parameter (here $t$), we must add the partial derivatives (sloppy: "the gradients").
Note: We have to add multiple path to the same variable as the multivariable chain rule tells us.
For the implementation we store the partial derivaties in a python dictionary.
We need a helper function combine_dicts for taking the multivariate chain rule into account:
import operator
def combine_dicts(a, b, op=operator.add):
x = (list(a.items()) + list(b.items()) +
[(k, op(a[k], b[k])) for k in set(b) & set(a)])
return {x[i][0]: x[i][1] for i in range(0, len(x))}
a = {'a': 2, 'b':3, 'c':4}
b = {'a': 5, 'c':6, 'x':7}
combine_dicts(a, b)
A = {'a':-1.3, 'b':-4, 'c':3}
B = {'b':3, 'c':4, 'd':5}
combine_dicts(A,B)
Autodiff class Scalar¶
The deep learning frameworks support automatic differentiation via backpropagation through the computational graph.
To demonstrate how autodiff works we implement a simple autodiff python class Scalar. For each operator we have to implement additionally how the operator is differentiated (grad):
class Scalar(object) :
"""Simple Scalar object that support autodiff."""
def __init__(self, value, name=None):
self.value = value
if name:
self.grad = lambda g : {name : g}
else:
self.grad = lambda g : {}
def __add__(self, other):
assert isinstance(other, Scalar)
# forward pass: addition is simple:
ret = Scalar(self.value + other.value)
#
def grad(g):
x = self.grad(g)
x = combine_dicts(x, other.grad(g))
return x
ret.grad = grad
return ret
def __mul__(self, other):
assert isinstance(other, Scalar)
ret = Scalar(self.value * other.value)
#
def grad(g):
x = self.grad(g * other.value)
x = combine_dicts(x, other.grad(g * self.value))
return x
ret.grad = grad
return ret
def square(self):
ret = Scalar(self.value**2)
#
def grad(g):
x = self.grad(2.0 * self.value * g)
return x
ret.grad = grad
return ret
+ (name='d')
/ \
(d./dc = g) / \
/ 1
/
|
* (name='c')
/ \
(d./da = b*g)/ \ (d./db = a*g)
/ \
a=1 b=2
g: backpropagated "gradient value" - in general different at each position
starts at the root of the tree with g = 1 (d root/d root = 1)Example: $$ d = (a * b) + 1 $$
$$ \frac{\partial d}{\partial a} = \frac{\partial (a*b+1)}{ \partial a} = b $$$$ \frac{\partial d}{\partial b} = \frac{\partial (a*b+1)}{ \partial b} = a $$a = Scalar(1., 'a')
b = Scalar(2., 'b')
c = b * a
d = c + Scalar(1.)
print (d.value)
# backpropagtion of the value 1 through the graph:
print ("derivatives of d:", d.grad(1))
Example Linear Regression with autodiff class¶
# generate some train data
x_min = -10.
x_max = 10.
m = 10
x = np.random.uniform(x_min, x_max, m)
a = 10.
c = 5.
y_noise_sigma = 3.
y = a + c * x + np.random.randn(len(x)) * y_noise_sigma
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(x, y, "bo")
plt.xlabel("x")
plt.ylabel("y")
# Univariate Linear Regression
# train data
x_values = x
y_values = y
# start values
b_value=15.; w_value=2.
assert x_values.shape[0] == y_values.shape[0]
nb_examples = x_values.shape[0]
def linear_model_with_data(b_value, w_value, x_values, y_values):
b = Scalar(b_value, name='b')
w = Scalar(w_value, name='w')
cost = Scalar(0.)
h = []
for x, y in zip(x_values, y_values):
h_ = b + w * Scalar(x)
diff = h_ + Scalar(-1.) * Scalar(y)
cost = cost + diff.square()
h.append(h_)
cost = cost * Scalar(1./nb_examples)
return h, cost
def get_linear_model(x_values, y_values):
return lambda b_value, w_value: linear_model_with_data(
b_value, w_value, x_values, y_values)
linear_model = get_linear_model(x_values, y_values)
h, cost = linear_model(b_value, w_value)
#print ([i.value for i in h] )
print (cost.value)
# Gradient Descent
learning_rate = 0.01
n_iterations = 200
costs = np.ndarray([n_iterations])
for i in range(n_iterations):
deltas = cost.grad(1.)
#print ("derivatives of cost:", cost.grad(1.))
b_value = b_value - learning_rate * deltas['b']
w_value = w_value - learning_rate * deltas['w']
h, cost = linear_model(b_value, w_value)
costs[i] = cost.value
#print ([i.value for i in h] )
print (b_value, w_value)
print (cost.value)
plt.plot(range(n_iterations), costs)
plt.xlabel("Iterations")
plt.ylabel("Cost")
plt.plot(x,y, "bo")
xx = np.array((-10.,10))
yy = b_value + w_value * xx
plt.plot(xx, yy, 'r-')
plt.xlabel("x")
plt.ylabel("y")
Gradients for vectorized operations¶
Example: Matrix Multiplication
# forward pass
theta = np.random.randn(6, 9)
x = np.random.randn(9, 4)
mprod = np.dot(theta, x) # shape [6, 4]
# gradient backproped down to mprop
grad_mprod = np.random.randn(*mprod.shape) # same shape as mprop
# Gradient calculation:
# shape of grad_theta has to be [6, 4]
grad_theta = np.dot(grad_mprod, x.T) #.T gives the transpose of the matrix
# shape of grad_x has to be [9,4]
grad_x = np.dot(theta.T, grad_mprod)
Autodiff for symbolic computation¶
An extra graph for computing the gradient is build.
Advantage: Separated optimization of the "gradient computational graph is possible".
from IPython.display import Image
Image(filename='pics/comp_graph_backward.png', height=400)
Gradient calculation with theano¶
# in theano each symbolic variable must be assigned a tensor (shape) type and data type
A = T.dscalar('A') # default of dtype is floatX
print ("A.dtype:", A.dtype)
B = T.dscalar('B')
C = T.mul(B, A)
D = C + 1
f = function(inputs=[A, B], outputs=D) # compile a function
dD_dA, dD_dB = T.grad(D, wrt=[A, B])
from theano import pp
print (pp(dD_dA)) # print out the gradient prior to optimization
print (pp(dD_dB))
grad_a = function(inputs=[A,B], outputs=dD_dA)
grad_b = function(inputs=[A,B], outputs=dD_dB)
grad_a(1,2)
grad_b(1,2)
Gradient calculation with TensorFlow¶
# if no graph is specified the default graph is used
A = tf.placeholder(name="A", dtype=tf.float32)
B = tf.placeholder(name="B", dtype=tf.float32)
C = tf.multiply(B, A, name="multiplication")
D = C + 1
help(tf.gradients)
grad = tf.gradients(D, [A, B])
#print (grad)
with tf.Session() as sess:
#sess.run(tf.initialize_all_variables())
print(sess.run(grad, feed_dict={A:5., B:3.}))
Exercise¶
Implement the univariate linear regression with tensorflow. Implement gradient descent with tf.gradients.
Note:
- Parameters of the models are typically implemented with (shared) variables. The gradient calculation with
tf.gradientsworks with variables in the same way as shown above. - To update a variable use
tf.assign:
v = tf.Variable(0., name="v")
c = tf.constant(0.1)
new_value = tf.add(v, c)
update = tf.assign(v, new_value)
init_op = tf.initialize_all_variables()
with tf.Session() as sess:
sess.run(init_op)
print(sess.run(v))
for _ in range(3):
sess.run(update)
print(sess.run(v))
Literature and Links:¶
Deep Learning Libraries¶
- Mxnet documentation: Programming Models for Deep Learning
- Symbolic computing and deep learning tutorial with Tensorflow / Theano
- Comparison of Theano with other deep learning framework
Backpropagation¶
- C. Olah: Calculus on Computational Graphs: Backpropagation - Blog Article
- Lecture Notes CS 231 Convolutional Neural Networks for Visual Recognition: Backpropagation
- [Bay15] Atilim Gunes Baydin, Barak A. Pearlmutter, Alexey Andreyevich Radul, Jeffrey Mark Siskind: Automatic differentiation in machine learning: a survey, arXiv preprint arXiv:1502.05767 (2015).
- [LM] Erik Learned-Miller: Vector, Matrix, and Tensor Derivatives