LSTM (Long Short Term Memory)¶
- Learning of recurrent neural networks by backpropagation-through-time
- Vanishing gradient problem [H91]
- LSTM was introduced by [SH97] to mitigating the vanishing gradient problem.
- Later Peephole Connections and Forget Units are added to the original LSTM algorithm for further improvement [GSC00] [FG01].
LSTM with forget gate and peephole connections¶
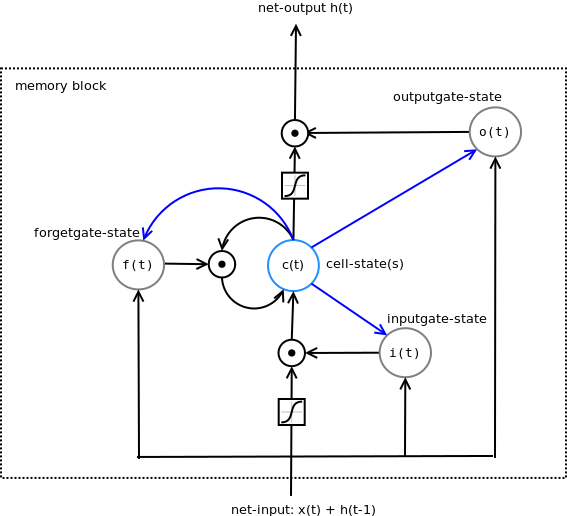
The blue arrows are the peephole connections. So the gates "see" the cell state(s) even if the output gate is closed.
LSTM forward pass with a cell per memory block¶
Input gates: $$ \vec i_t = \sigma( \vec x_t W_{xi} + \vec h_{t-1} W_{hi} + \vec c_{t-1} W_{ci} + \vec b_i) $$
Forget gates: $$ \vec f_t = \sigma (\vec x_t W_{xf} + \vec h_{t-1} W_{hf} + \vec c_{t-1} W_{cf} + \vec b_f) $$
Cell units: $$ \vec c_t = \vec f_t \circ \vec c_{t-1} + \vec i_t \circ \tanh(\vec x_t W_{xc} +\vec h_{t-1} W_{hc} + \vec b_c) $$
Output gates: $$ \vec o_t = \sigma(\vec x_t W_{xo}+ \vec h_{t-1} W_{ho} + \vec c_t W_{co} + \vec b_o) $$
The hidden activation (output of the cell) is also given by a product of two terms:
$$ \vec h_t = \vec o_t \circ \tanh (\vec c_t) $$# squashing of the gates should result in values between 0 and 1
# therefore we use the logistic function
sigma = lambda x: 1 / (1 + T.exp(-x))
# for the other activation function we use the tanh
act = T.tanh
# sequences: x_t
# prior results: h_tm1, c_tm1
# non-sequences: W_xi, W_hi, W_ci, b_i, W_xf, W_hf, W_cf, b_f, W_xc, W_hc,
# b_c, W_xo, W_ho, W_co, b_o, W_hy, b_y
def one_lstm_step(x_t, h_tm1, c_tm1, W_xi, W_hi,
W_ci, b_i, W_xf, W_hf,
W_cf, b_f, W_xc, W_hc,
b_c, W_xo, W_ho, W_co,
b_o, W_hy, b_y):
i_t = sigma(theano.dot(x_t, W_xi) + theano.dot(h_tm1, W_hi) + theano.dot(c_tm1, W_ci) + b_i)
f_t = sigma(theano.dot(x_t, W_xf) + theano.dot(h_tm1, W_hf) + theano.dot(c_tm1, W_cf) + b_f)
c_t = f_t * c_tm1 + i_t * act(theano.dot(x_t, W_xc) + theano.dot(h_tm1, W_hc) + b_c)
o_t = sigma(theano.dot(x_t, W_xo)+ theano.dot(h_tm1, W_ho) + theano.dot(c_t, W_co) + b_o)
h_t = o_t * act(c_t)
y_t = sigma(theano.dot(h_t, W_hy) + b_y)
return [h_t, c_t, y_t]
Let's plot the error over the epochs:
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(np.arange(nb_epochs), train_errors, 'b-')
plt.xlabel('epochs')
plt.ylabel('error')
plt.ylim(0., 50)
(0.0, 50)
Prediction¶
We need a new theano function for prediction.
So we can check, if the second to last target is correct. This is the long range dependency.
def print_out(test_data):
for i,o in test_data:
p = predictions(i)
print o[-2] # target
print p[-2] # prediction
print
print_out(test_data)
[ 0. 1. 0. 0. 0. 0. 0.] [ 5.87341716e-08 9.98579154e-01 4.88535012e-04 4.44523958e-04 7.67934429e-03 2.87055787e-03 6.28327452e-07] [ 0. 0. 0. 0. 1. 0. 0.] [ 5.52932574e-07 2.15697982e-03 2.67693579e-06 2.32383549e-06 9.97944801e-01 3.53073188e-04 1.68163507e-03] [ 0. 0. 0. 0. 1. 0. 0.] [ 4.96641009e-07 2.53249861e-03 4.70637517e-06 4.04892606e-06 9.97504234e-01 3.63369503e-04 9.02570554e-04] [ 0. 1. 0. 0. 0. 0. 0.] [ 5.23470983e-08 9.98680073e-01 9.35965260e-04 8.49713090e-04 5.20350603e-03 3.27583924e-03 3.63178526e-07] [ 0. 1. 0. 0. 0. 0. 0.] [ 4.81470559e-08 9.99168377e-01 1.26687233e-03 1.14786959e-03 3.51463269e-03 3.45002380e-03 2.44450194e-07] [ 0. 1. 0. 0. 0. 0. 0.] [ 4.60820845e-08 9.99167152e-01 1.65640502e-03 1.49691757e-03 3.68675213e-03 3.56958504e-03 1.90461928e-07] [ 0. 1. 0. 0. 0. 0. 0.] [ 4.85837261e-08 9.99094814e-01 1.22654396e-03 1.10715044e-03 4.06259123e-03 3.24962910e-03 2.37590269e-07] [ 0. 1. 0. 0. 0. 0. 0.] [ 4.26216336e-08 9.99066073e-01 3.04143221e-03 2.75796126e-03 3.23995209e-03 4.38898326e-03 1.40485394e-07] [ 0. 1. 0. 0. 0. 0. 0.] [ 5.11170010e-08 9.99252047e-01 7.74864194e-04 7.03969285e-04 4.32425542e-03 3.25879540e-03 3.57672809e-07] [ 0. 0. 0. 0. 1. 0. 0.] [ 5.96127827e-07 2.12697616e-03 7.98416652e-06 6.89350153e-06 9.97370635e-01 5.55196261e-04 2.06753946e-03]
Literature¶
[SH97] [S. Hochreiter, J. Schmidhuber: Long Short-Term Memory, Neural Computation 9(8), 1997](http://deeplearning.cs.cmu.edu/pdfs/Hochreiter97_lstm.pdf
[H91] S. Hochreiter. Untersuchungen zu dynamischen neuronalen Netzen. Diploma thesis, Institut f. Informatik, Technische Univ. Munich, 1991. Advisor: J. Schmidhuber
[FG01] F.Gers: Long Short-Term Memory in Recurrent Neural Networks, Phd Thesis, Lausanne 2001
[AG14] Alex Graves: Generating sequences with recurrent neural networks