Bias Variance Tradeoff

Model complexity and generalization

Learning Objectives

Concepts of machine learning

  • Target function
  • Overfitting, underfitting
  • Generalization
  • Out-of-sample error and test data
  • Model complexity

Target function and noise

For prediction: We want to approximate an unknown function, the target function $t(\vec x)$.

If the targets $y$ would be deterministically determined from the $\vec x$ values:

$$ y = t(\vec {x}) $$

But $y$ is typically noisy. We can model this by:

$$ y^{(i)} = t(\vec {x}^{(i)}) + \epsilon $$

with a random variable $\epsilon$ (= stochastic noise)

Sidenote:

Instead of a function we now a a (conditional) probability distribution: $$ p(y \mid \vec {x}) $$

The probability distribution of the noise can depend on $\vec {x}$: $p(\epsilon \mid \vec {x})$.

Goal:

We are looking for "good" hypotheses. $$ h(\vec x) \approx t(\vec x) $$ for all $\vec{x}$ of interest, i.e. for all possible $\vec{x}$ we want to predict. ($p(\vec x)$ suffient large).

Training data is noisy: $y^{(i)} = t(\vec {x}^{(i)}) + \epsilon $

Therefore $h(\vec{x}^{(i)})$ should not perfectly match $y^{(i)}$ of the training data.
But how good should be the correspondence?

Sampling Error

  • Which pattern are caused by the target function?
  • Which pattern are caused by the (random chosen) train data?

Overfitting and Underfitting

In [1]:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
In [2]:
import numpy as np

def test_func(f, x, err=1.):
    return np.random.normal(f(x), err)

def compute_error(x, y, p):
    yfit = np.polyval(p, x)
    return np.sqrt(np.mean((y - yfit) ** 2))
    
    
def plot_under_overfit_polynoms():
    N = 10
    np.random.seed(45)
    x = np.linspace(-4, 3., N)
    quadratic_func = lambda x: -2 + 3. * x + -2. * x**2
    y = test_func(quadratic_func,x, 4.)

    xfit = np.linspace(-4, 3., 1000)

    degrees = [1, 2, 9]
    titles = ['d = 1 (under-fit)', 'd = 2', 'd = '+ str(degrees[2]) + ' (over-fit)']


    plt.figure(figsize = (9, 3.5))
    plt.subplots_adjust(left = 0.06, right=0.98,
                   bottom=0.15, top=0.85,
                   wspace=0.05)
    yticks = [-50,-40,-30,-20,-10, 0, 10]
    for i, d in enumerate(degrees):
        plt.subplot(131 + i, yticks=yticks)
        yticks=[]
        plt.scatter(x, y, marker='x', c='k', s=50)

        p = np.polyfit(x, y, d)
        yfit = np.polyval(p, xfit)
        plt.plot(xfit, yfit, '-b')
    
        #pl.xlim(-0.2, 1.2)
        plt.ylim(-55, 15)
        plt.xlabel(u'x')
        if i == 0:
            plt.ylabel('y')
        plt.title(titles[i])

Example: Linear Regression with polynominal basis functions

In [3]:
plot_under_overfit_polynoms()

Example: Classification Underfitting

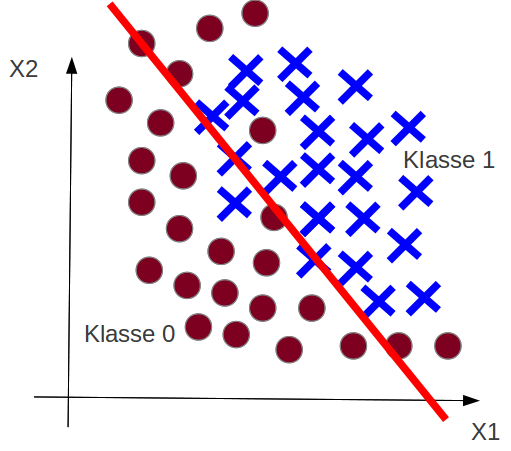
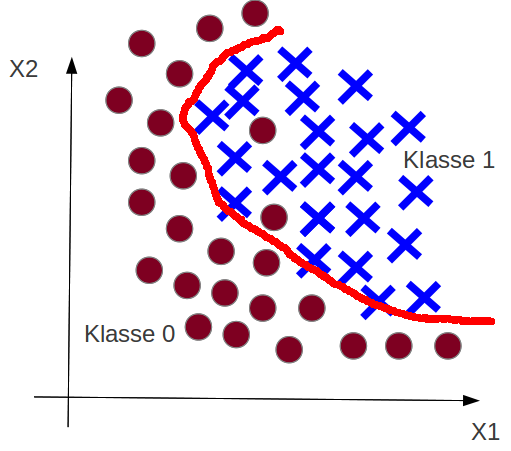
Example: Classification Overfitting

Example: Just Right

Goal of learning - Hypothesis Set $\mathcal{H}$}

Goal of learning: We are looking for a appropriate hypothesis $$ h(\vec x) \approx t(\vec x) $$

$h$ is determined from the hypothesis set $\mathcal{H}$ by training.

Example ``Univariate Linear Regression'':

$\mathcal H$ is the set of all (infinit) hypotheses: $h_\theta(x) = \theta_0 + \theta_1 x$ (by variation of $\theta_0$ and $\theta_1$).

From the set $\mathcal{H}$ we get through training a $\theta$, i.e. a hypothesis $h_{\theta_{final}}({x})$.

$h_{\theta_{final}}({\bf x})$ is given by the minimum of the cost function:

$\forall \theta: J(\theta_{final}) \leq J(\theta)$

Underfitting

Recap: Goal is $h(\vec x) \approx t(\vec x)$.

What happens in the underfitting case?

The goal can not be reached: No hypothesis of $\mathcal{H}$ is similar enough to $t(\vec x)$.

The hypothesis set $\mathcal{H}$ has not suffient complexity.

Overfitting

Recap: Goal is $h(\vec x) \approx t(\vec x)$.

What happens in the overfitting case?

The trained hypothesis $h_{\theta_{final}}({x})$ is adaped to much on the training data: also on the noise pattern.

The hypothesis set $\mathcal{H}$ has to much complexity.

Test data

Training error

Up to now only a training set $\mathcal{D}_{train}$ and calculation of the average loss of the traing data (cost function):

Training error (in-sample error $E_{in}(h)$):

$$ E_{in}(h) = \frac{1}{m} \sum_{i=0}^{m} loss(h(\vec x^{(i)}), y^{(i)}) $$

Note: We consider $E_{in}(h)$ now as a function of possible hypotheses $h$. We want to compare different models.

The low training error is not suffient to judge a "good" model.

Overfitting!

$h(\vec x)$ can make bad predictions for $\vec x$ values not in the training set.

Bad generalization.

Out-of-sample error

The out-of-sample error is the average loss of typical (new) data ($p({\vec x}', y')$ suffient large):

$$ E_{out}(h) = \mathbb{E}_{\bf x,y}\left[loss(h({\vec x}), y)\right] = \int\limits_{\mathcal{X \times Y}} loss(h({\vec x}), y) dp({\vec x},y) $$

Generalization error

The generalization error of a hypothesis $h$ can defined as (after [Abu]):

$$ | E_{out}(h) - E_{in}(h)| $$

Test data

Problem: We can compute the out-of-sample error $E_{out}$ directly.

Take $m_{test}$ labeled test data $\mathcal{D}_{test}$ to check if $h(\vec x)$ predicts good values even for $\vec x$ values not used in training.

$$ \mathcal{D}_{test}= \{ ( {\vec {x'}}^{(0)}, {y'}^{(0)} ), ( {\vec {x'}}^{(1)}, {y'}^{(1)} ), \dots, ( {\vec {x'}}^{(m_{test})}, {y'}^{(m_{test})} ) \} $$

Test error

The test error is the average loss of the test data:

$$ testerror = \frac{1}{m'} \sum_{i=0}^{m_{test}} loss(h({\vec {x'}}^{(i)}), {y'}^{(i)}) $$

The test error is an approximation of the out-of-sample error $E_{out}(h)$:
$$ testerror \approx \mathbb{E}_{\mathcal{X,Y}}[loss(h({\bf x}), y)] = E_{out}(h) $$

Model complexity, Capacity

informal:

The complexity of $\mathcal{H}$ describes how many compex functions the hypothesis set $\mathcal{H}$ can cover.

Measure of model complexity are

  • VC-Dimension $d_{vc}$ (Vapnik–Chervonenkis Dimension)
  • Rademacher complexity

Expectation of out-of-sample error

Starting point for the Bias-Variance Analysis is the expectation of out-of-sample error:

$$ \mathbb{E}_{\mathcal{D}} \left[ E_{out}(h^{\mathcal{D}}({\bf x})) \right] $$

with

  • $h^{\mathcal{D}}$: trained hypothesis from $\mathcal{D}$ (training data)
  • $E_{out}(h^{\mathcal{D}})$: out-of-sample error for the trained hypothesis
  • $\mathbb{E}_{\mathcal{D}}$: Expectation with respect to the training data (a training set is an event).

Bias-variance analysis

without noise and squared error: \begin{align*} \mathbb{E}_{\mathcal{D}} \left[ E_{out}(h^{\mathcal{D}}) \right] & = \mathbb{E}_{\mathcal{D}} \left[ \mathbb{E}_{\bf x,y} \left[ \left(h^{\mathcal{D}}({\bf x}) - t({\bf x})\right)^2 \right] \right] \\ & = \mathbb{E}_{\bf x,y} \left[ \mathbb{E}_{\mathcal{D}} \left[ \left(h^{\mathcal{D}}({\bf x}) - t({\bf x})\right)^2 \right] \right] \end{align*}

with the average hypothesis $$ \tilde{h}({\bf x}) = \mathbb{E}_{\mathcal{D}}\left[ h^{\mathcal{D}}({\bf x}) \right] $$

We get (see e.g. [Abu] p.63): \begin{align*} \mathbb{E}_{\mathcal{D}} \left[ E_{out}(h^{\mathcal{D}}({\bf x})) \right] &= \mathbb{E}_{\bf x,y} \left[ \mathbb{E}_{\mathcal{D}} \left[\left(h^{\mathcal{D}}({\bf x}) - \tilde{h}({\bf x}) \right)^2\right]\right] &+&\mathbb{E}_{\bf x,y} \left[ \left(\tilde{h}({\bf x}) -t({\bf x}) \right)^2 \right]& \\ &= variance &+&bias^2 \end{align*}

with noisy data there is a thrid term: the irreducable error $\mathbb{E}_{\mathcal X}[\epsilon^2]$ (Bayes Error, see e.g. [Has])}

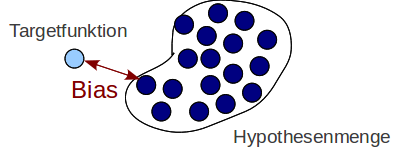
Interpretation: Bias

$$ \mathbb{E}_{\bf x,y} \left[ \left(\tilde{h}({\bf x}) -t({\bf x}) \right)^2 \right] $$ Quadratic deviation of the average hypothesis $\tilde h$ from the target function $t$ $\leftrightarrow$ Underfitting

Interpretation: Variance

$$ \mathbb{E}_{\bf x,y} \left[ \mathbb{E}_{\mathcal{D}} \left[\left(h^{\mathcal{D}}({\bf x}) - \tilde{h}({\bf x}) \right)^2\right]\right] $$

Average quadratic deviation {$h^{\mathcal{D}}$} from the average hyposesis $\tilde h$ $\leftrightarrow$ Overfitting

Example

from [Abu]

  • Target function $sin(x)$
  • $p(x)$: Uniform distributed in the range $(0, 2 \pi)$
  • no noise
  • only two training examples. i.e. $n=2$
  • Model 1: $h(x)=w$ (constant)
  • Model 2: $h(x)=\theta_0 + \theta_1 x$

Exercise

Approximate: $\mathbb E (E_{out})$, the bias and the variance for both models by sampling. A sample correspond to a training set (with 2 examples)

In [5]:
x, y  = train_data()
theta_0, theta_1 = get_theta(x, y)
plt.plot(x_, y_, 'b-')
plt.scatter(x,y,color='r')
plt.plot(x_,  theta_0 + theta_1 * x_, 'g-')
Out[5]:
[<matplotlib.lines.Line2D at 0x10ef89358>]

No noise on $y$ : $$ \mathbb E_{\bf x, \bf y} [ E_{out} ] = \int_{-\infty}^{\infty} (t(x)- h(x))^2 p(x) dx = \int_{0}^{2 \pi} (t(x)- h(x))^2 dx $$

In [8]:
expectation_Eout_1 = e_out_m1.mean()
print ("expectation of E_out of model 1:", expectation_Eout_1)

expectation of E_out of model 1: 0.7495649709872853
In [9]:
expectation_Eout_2 = e_out_m2.mean()
print ("expectation of E_out of model 2:", expectation_Eout_2)

expectation of E_out of model 2: 1.8852093027834775
In [10]:
# Average Model 1 and 2 
plt.plot(x_, y_, 'b-', label='target function')
plt.plot(x_,  avg_theta_0 + avg_theta_1 * x_, 'r-', label='average model 2')
plt.plot(x_,  np.ones(len(x_)) * avg_w, 'g-', label='average model 1')
plt.xlabel("x"); plt.ylabel("y"), plt.legend()
Out[10]:
(<matplotlib.text.Text at 0x10efc5438>,
 <matplotlib.legend.Legend at 0x10f4379e8>)

From the plot we see that the bias of model 2 is smaller than the bias of model 1.

In [12]:
print ("Bias of model 1:", bias_1)

Bias of model 1: 0.4994622029361333
In [14]:
print ("Bias of model 2:", bias_2)

Bias of model 2: 0.20764158671729008
In [17]:
print ("Variance of model 1:", variance_1)

Variance of model 1: 0.2502570759559479
In [19]:
print ("Variance of model 2:", variance_2)

Variance of model 2: 1.6858020395241051
In [20]:
print("model 1: E_out ≈ bias + variance:  %f ≈ %f + %f" % (expectation_Eout_1, bias_1, variance_1))
print("model 2: E_out ≈ bias + variance:  %f ≈ %f + %f" % (expectation_Eout_2, bias_2, variance_2))

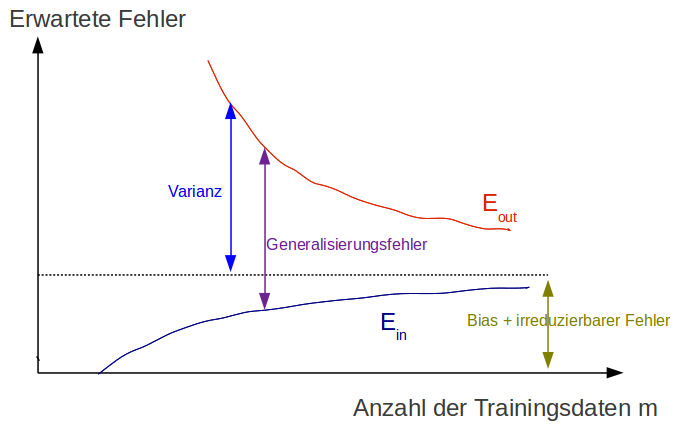
model 1: E_out ≈ bias + variance:  0.749565 ≈ 0.499462 + 0.250257
model 2: E_out ≈ bias + variance:  1.885209 ≈ 0.207642 + 1.685802

Learning curves

Goal

$$ h(\vec x) \approx t(\vec x) $$ reached if $E_{out}$ is small (small test error)

Both conditions must be satisfied

  • $E_{in}$ small training error (low bias, no underfitting)
  • Small generalization error $|E_{out} -E_{in}|$ respectively $test error \approx trainings error$ (low variance, no overfitting)

How can we know that the model is adequate?

Adequate in respect to:

  • Number of training data $m$ of $\mathcal{D}_{train}$
  • Model complexity $\mathcal{H}$
  • Signal-noise ration: strength of stochastic noise $\epsilon$ in respect to the target function $t$

Learning curve of a simple model

Learning curve of a complex model

Literature: